Computational Methods in Solid State Physics
Nemoshkalenko V V, Antonov N V
1.1 Cround State of a Many-Electron System
电子在凝聚相体系中的运动是高度相关的(highly correlated)。首先,使用独立粒子近似不能描述这样的体系。然而,我们可以使用无相互作用粒子的模型系统,在该模型中,总能量E和电子密度$\rho(r^2)$有相似的真实系统的函数,并且,所有的电子相互作用的效果被描述为一个外场(external field)。这就是密度泛函理论的本质。在介绍密度泛函理论之前,首先要先简短地介绍由Hartree,Fock和Slater发展的自洽场方法(self-consistent field)。
1.1.1 Hartree-Fock Equations
Hartree最根本的贡献是提出:每一个电子的运动都是在原子核外场下独立于其他电子的运动,某个给定的电子与其他电子的相互作用可以用该电子与这些电子态的平均电荷密度诱导的静电场的作用所代替。在这里,每个电子都被分配了一个单独的函数$\varphi_{i}$,即一个轨道,而一个电子系统的完整波函数被表示为所有轨道的乘积。然后,该轨道的单电子方程为:
\[\hat{F}_{i} \varphi_{i}(\vec{r})=\varepsilon_{i} \varphi_{i}(\vec{r}) \qquad (1.1)\] \[\hat{F}_{i}=-\nabla^{2}+V_{C}(\vec{r})+V_{i}(\vec{r}) \qquad (1.2)\]这里,$\nabla^{2}$是动能算符,$V_{C}(\vec{r})$是一个电子在$\vec{r}$点处的库伦势能(Coulomb potential energy),这个势能是由该电子与原子核的相互作用和与给定系统的所有电子的总的电荷密度的相互作用。为了补偿自相互作用(self-interaction)相互作用,我们需要如下的能量:
\[V_{i}(\vec{r})=-n_{i} \int 2 \frac{\varphi_{i}^{*}\left(\vec{r}^{\prime}\right) \varphi_{i}\left(\vec{r}^{\prime}\right)}{\left|\vec{r}-\vec{r}^{\prime}\right|} d \vec{r}^{\prime} \qquad (1.3)\]在这里,$n_{i}$是第$i$个轨道中填充的电子数。
当一个原子中有$Z$个核电荷数,此时,库伦势为:
\[V_{C}(\vec{r})=-\frac{2 Z}{r}+\sum_{j} n_{j} \int 2 \frac{\varphi_{i}^{*}\left(\vec{r}^{\prime}\right) \varphi_{j}\left(\vec{r}^{\prime}\right)}{\left|\vec{r}-\vec{r}^{\prime}\right|} d \vec{r}^{\prime} \qquad (1.4 )\]因此,对于一个包含$N$个电子的体系,每个电子都受到由原子核和 N-1 电子引起的场的作用。
Hartree方程允许我们使用函数$\varphi_{i}$写能量泛函行列式。$\varphi_{i}$需要使用方程(1.1)自洽求解,必须要最小化该函数。Fock和Slater利用上述方程(1.1)的解构建了Hartree-Fock方程。
根据Pauli原则,体系的总波函数应该满足关于电子对交换的反对称性原则。Hartree-Fock理论是通过近似使用行列式表示多电子波函数来满足Pauli原则的:
\[\Psi\left(\vec{r}_{1}, \vec{r}_{2}, \ldots, \vec{r}_{N}\right)=\frac{1}{\sqrt{N !}}\left|\begin{array}{cccc}\varphi_{1}\left(\vec{r}_{1}\right) & \varphi_{1}\left(\vec{r}_{2}\right) & \ldots & \varphi_{1}\left(\vec{r}_{N}\right) \\\varphi_{2}\left(\vec{r}_{1}\right) & \varphi_{2}\left(\vec{r}_{2}\right) & \ldots & \varphi_{2}\left(\vec{r}_{N}\right) \\\vdots & \vdots & \ddots & \vdots \\\varphi_{N}\left(\vec{r}_{1}\right) & \varphi_{N}\left(\vec{r}_{2}\right) & \ldots & \varphi_{N}\left(\vec{r}_{N}\right)\end{array}\right| \qquad (1.5)\]把上述多电子波函数带入到薛定谔方程中,使用Ritz变分原理:
\[\delta\left[\frac{\int \Psi^{*}(\mathbf{H}-E) \Psi d V}{\int \Psi^{*} \Psi d V}\right]=0 \qquad (1.6)\]并考虑到轨道正交化的所有条件,我们得到 Hartree-Fock 方程:
\[\left[-\nabla^{2}+V_{C}(\vec{r})\right] \varphi_{i}(\vec{r})-\sum_{j} n_{j} \varphi_{j}(\vec{r}) \int 2 \frac{\varphi_{j}^{*}\left(\vec{r}^{\prime}\right) \varphi_{i}\left(\vec{r}^{\prime}\right)}{\left|\vec{r}-\vec{r}^{\prime}\right|} d \vec{r}^{\prime}=\varepsilon_{i} \varphi_{i}(\vec{r}) \qquad (1.7)\]这个方程中的求和是在平行自旋电子的状态上进行的。上式中的第一项与Hartree方程中的相同(1.1,1.2)。左边的最后一项描述的是交换相互作用,也是一种库伦相互作用,与使用(1.5)形式的波函数产生的电子运动的相关性有关。请注意,如果在交换项中只剩下 j=i 的分量而不是对 j 的求和,则该项将与 Hartree方程(1.3)中的$V_{i}(\vec{r})$相同,该项描述的是一个电子与其自身的相互作用。因此,很明显,Hartree-Fock 方法中的交换修正包括描述自相互作用的项和$i \neq j$的项,即交换项。
Hartree-Fock方程最方便的形式是公式(1.1)。我们得到了$\hat{F}_{i}$算符:
\[\hat{F}_{i}=-\nabla^{2}+V_{C}(\vec{r})+V_{\mathrm{x} i}(\vec{r}) \qquad (1.8)\]其中$V_{\mathrm{x} i}(\vec{r})$为:
\[V_{\mathrm{x} i}(\vec{r})=-\frac{\sum_{j} n_{j} \int d \vec{r}^{\prime} 2 \varphi_{i}^{*}(\vec{r}) \varphi_{j}^{*}\left(\vec{r}^{\prime}\right) \varphi_{j}(\vec{r}) \varphi_{i}\left(\vec{r}^{\prime}\right) /\left|\vec{r}-\vec{r}^{\prime}\right|}{\varphi_{i}^{*}(\vec{r}) \varphi_{i}(\vec{r})} \qquad (1.9)\]交换电势$V_{\mathrm{x} i}(\vec{r})$是一个远离空穴的电子的电荷电势。因此,Hartree-Fock 方程可以解释为 Hartree 方程,即一个单独的电子在原子核和整个电子电荷的场中运动,大小与电子相等的交换电荷场会使该场衰减,交换电荷场局域在给定电子周围的费米空穴处。
式(1.8)中的算符$\hat{F_i}$依赖于轨道,这使Hartree-Fock方程的解变得复杂。因此,后者与通常通过迭代技术求解的非线性微积分方程有关。首先,选择初始的轨道$\varphi_{i}(\vec{r})$ 基组,带入公式(1.8),然后,求解本征值,定义另一组轨道,从而实现自洽。
目前,Hartree-Fock方法是最好的单电子方法。然而,它在计算有限多粒子系统(即原子)的电子结构方面也是最有效的。
然而,应用在宏观的多电子系统中仍然很困难,即使是自由电子气。自由电子气的交换关联势与函数$F(k/k_{F})$成正比,该函数在费米分布的底部具有统一性,在峰值处是1/2,在激发态区域是0。因为交换能是负的,当它被包括在内时,费米分布底部的能级数和态密度大大降低。Figure 1.1是包含交换关联能计算的一个自由电子系统的态密度。在不考虑交换的情况下,态密度不再与能量的平方根成正比,而是在费米球上变为零。这与金属低温热容的实验数据相矛盾。
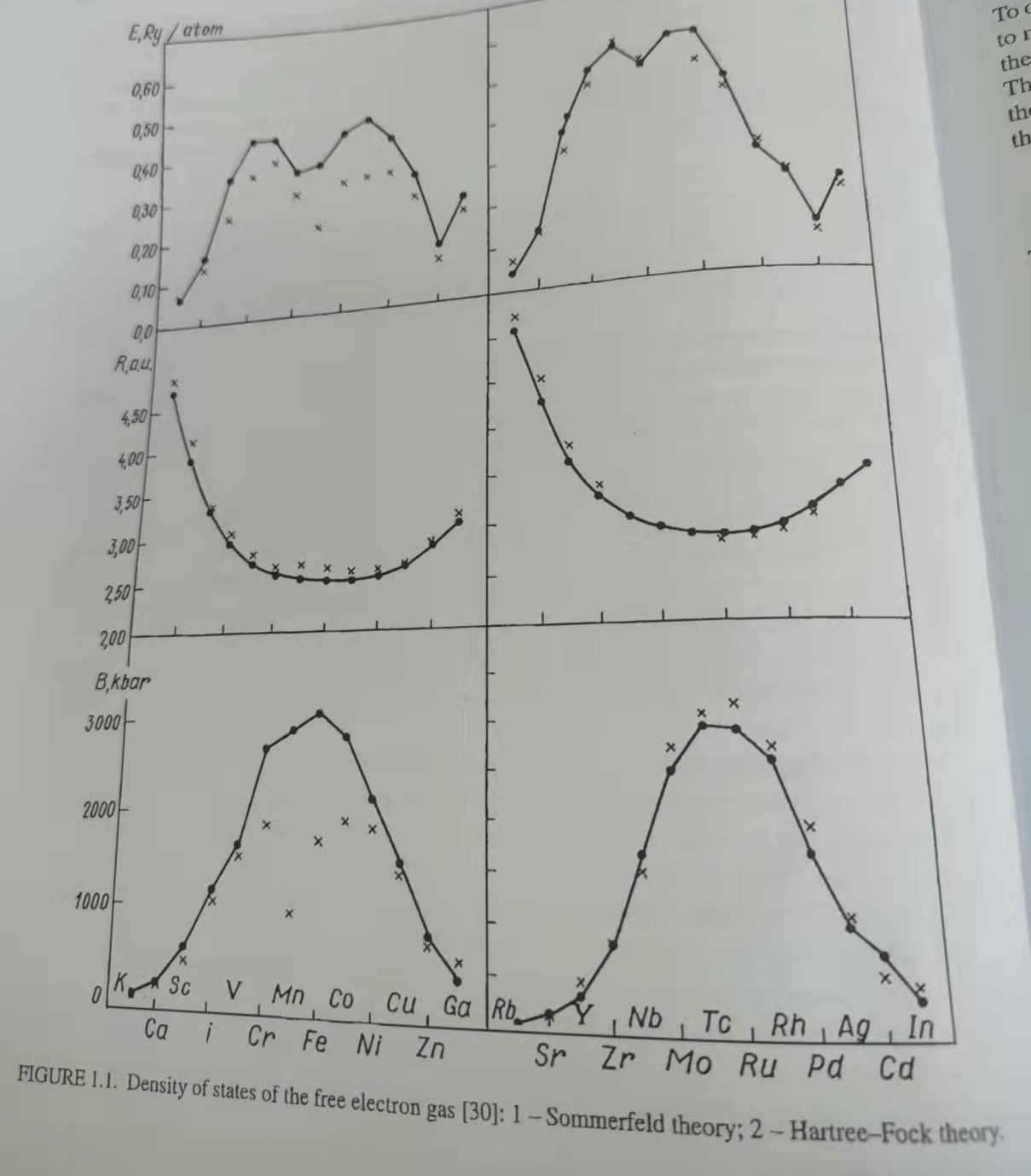
这种效应与库仑场的长程效应有关。之前已经提到,金属中的等离子基元激发为与高能区,属于紫外范围,因此在一般温度下它们不会被激发。由于存在屏蔽效应,电子-电子相互作用能可以使用如下势能定义,$V(r)\sim(1/r)e^{-\kappa r}$,其中$\kappa$是常数,而不是通过库伦势能。因此,电势在小于晶格常数的距离处呈指数下降。当电子间相互作用较大时,只存在一个平均的电子-电子相互作用。因此,在Hartree-Fock理论中,当交换能强烈依赖于$\vec{k}$时,Hartree-Fock 确定的单电子能量对于宏观系统的费米统计是不正确的。
然而,随着一般的交换矫正(仅仅依赖于$\vec{r}$)取代交换项(1.9)时,在很多情况下,理论可以取得和实验相符的结果。这就是Slater提出的$\chi_{\alpha}$方法所作的事情。
Reference
- Nemoshkalenko V V, Antonov N V. Computational methods in solid state physics[M]. CRC Press, 1999.