Computational Methods in Solid State Physics
Nemoshkalenko V V, Antonov N V
1.1 Cround State of a Many-Electron System
1.1.2 Slater $\chi_\alpha$ Approximate
为了获得对于所有电子态都相同的交换势能,Slater 提出用加权平均值代替交换项(1.9式),加权平均值对应于在点 $\vec{r}$ 处由第 $i$个轨道描述的电子的存在概率[ref-31]。由第$i$条轨道在点 $\vec{r}$ 处产生的电荷密度为:$n_i\varphi_i^{\ast}(\vec{r}) \varphi_{i}(\vec{r})$,在该点电子总的电荷密度为: ${\textstyle \sum_{k}} n_k \varphi_k^{\ast}(\vec{r}) \varphi_{k}(\vec{r})$。因此,$\vec{r}$ 处的电子处于第$i$条轨道所描述的态的概率为:
\[\frac{n_i \varphi_i ^ {\ast}(\vec{r}) \varphi_i(\vec{r})} { {\textstyle \sum_{k}} n_k \varphi_k ^ {\ast} (\vec{r}) \varphi(\vec{r}) } \qquad (1.10)\]然后,需要的加权平均值为:
\[V_{\mathrm{x}}=-\frac{\sum_{i} \sum_{j} n_{i} n_{j} \int \varphi_{i}^{*}(\vec{r}) \varphi_{i}\left(\vec{r}^{\prime}\right)\left(2 /\left|\vec{r}-\vec{r}^{\prime}\right|\right) \varphi_{j}^{*}\left(\vec{r}^{\prime}\right) \varphi_{j}(\vec{r}) d \vec{r}^{\prime}}{\sum_{k} n_{k} \varphi_{k}^{*}(\vec{r}) \varphi_{k}(\vec{r})} \qquad(1.11)\]现在,该势能对于所有电子态都是相同的。因此,公式1.8和1.9变为:
\[\left[-\nabla^{2}+V_{\mathrm{C}}(\vec{r})+V_{\mathrm{X}}(\vec{r})\right] \varphi_{i}(\vec{r})=\varepsilon_{i} \varphi_{i}(\vec{r}) \qquad (1.12)\]需要注意的是:平均的交换势能(1.11)不仅是Hartree-Fock方法的简化,而且也克服了Hartree-Fock方法在固体中决定能带能量的困难。因此,(1.12)中一个重要的特性是波函数是相互正交的,电子在其他电子产生的平均场中运动。在自由电子气中,(1.9)和(1.11)的交换势能可以被精确求解,此时Hartree-Fock的波函数是平面波。自由电子气的基态在动量空间中是一个半径为$k_F$的费米球(Fermi sphere)。一个波数为$k$的态的交换势能定义为:
\[V_{\mathrm{X}}(k)=-8\left(\frac{3}{8 \pi} \rho\right)^{1 / 3} F(\eta) \qquad (1.13)\]这里$\eta=k/k_F$,其中
\[F(\eta)=\frac{1}{2}+\frac{1-\eta^{2}}{4 \eta} \ln \left|\frac{1+\eta}{1-\eta}\right| \qquad (1.14)\]当$\eta=1(k=k_F)$时,函数$F(\eta)$存在对数奇点,这会导致在费米能级初的电子态密度为零,这和之前探讨的不同,与Hartree-Fock理论的结果不同,也与实验中关于电子热熔和磁化率的数据不相符。为了获得自由电子气的势能(1.11),我们必须对所有的占据态到$k=k_F$求平均。因为在$\eta$和$\eta+d\eta$之间的电子态与$\eta^2 d\eta$成正比,我们有:
\[F(\eta)=\frac{\int_{0}^{1} \eta^{2} F(\eta) d \eta}{\int_{0}^{1} \eta^{2} d \eta}=\frac{3}{4}\]现在我们得到:
\[V_{X}=-6\left(\frac{3}{8 \pi} \rho\right)^{1 / 3} \qquad (1.15)\]这个平均的交换势能依赖电子电荷密度,就自由电子气而言,电子电荷密度是常数。这是由Slater提出的,与一般情况相似,当电荷密度不均匀时,平均的交换势能可以自由电子气的势能近似得到,但是要使用局域的电子密度$\rho(\vec{r}) = {\textstyle \sum_{i}} \varphi_i^{\ast}(\vec{r}) \varphi_{i}(\vec{r})$
\[V_{\mathrm{XS}}(\vec{r})=-6\left(\frac{3}{8 \pi} \rho(\vec{r})\right)^{1 / 3} \qquad (1.16)\]这就是所谓的Slater交换势能。因为Slater提出在计算能带时使用(1.16)的交换势能,在多种体系中,很多电子结构和物理性质的计算才得以进行。在很多情况下,实验上观测到的结果与实验相符,尤其是对于纯的过渡金属。需要注意的是:这个势能描述基态特性(电子密度,总能量,晶格参数,费米面拓扑结构)和金属的激发态特性(X射线发射,光谱等)是非常方便的,
然而我们应该指出,Slater使用平均交换势能很难被认为是严格的。这是因为:在量子力学中,平均(作为一个近似)只有当物理上可观察的量被平均时才有物理意义。因此,Slater的方法是一种现象学的方法,包含交换势能(1.16)的(1.12)式被认为是单粒子(one-particle)方程,而不是单电子(one-electron)方程。
随后,密度泛函理论被提出,是在由Hartree,Fock,和Slater等人提出的自洽场的理论基础上产生的。Slater近似可以作为一种特殊的电子密度泛函获得:
\[E_{XC}[\rho]=\frac{3}{2} \int \rho(\vec{r}) \varepsilon_X(\rho) d\vec{r}\qquad (1.17)\]$\varepsilon_X(\rho)$是一个均匀系统的能量。因此,当我们只考虑交换效应而忽略关联效应时,使用DFT得到的能量与Slater势能只差了一个$\frac{3}{2}$的因子。这就是Gaspar-Kohn-Sham交换势能。这种差别可以解释为:在推导hartree-Fock方程时,Slater从总能量的行列式开始,在该表示中,轨道$\varphi_i$发生变化以尽量使总能量最小化,该程序导致了(1.8)式,然后交换势能$V_{Xi}(\vec{r})$(1.9)被平均的表达式(1.11)取代,然后用它的统计等价物(1.16)取代。与此相反,Gasper,Kohn和Sham使用统计近似的方式给出总能量的表达式,然后,改变$\varphi_i$函数来获得一个单电子方程。在这里,(1.12)中,而除了(1.16)中的$V_X(\vec{r})$,对于交换部分,只可以获得这个量的$\frac{3}{2}$。换句话来说,总能量的变化和交换成分的统计等价替换者这两个算符不对易。
Gasper,Kohn和Sham的结果也可以从Hartree-Fock中得到,在$k=k_F$处,比如在费米面上,用交换势能的真实值取代(1.13)中的势能即可。这种情况,$F(1)=1/2$。在物理上,可以这样理解:靠近费米能级的电子的分布决定了电子密度的顺序。因此,Slater方法就是在所有占据能级上对交换势能求平均,然而,Gaspar,Kohn和Sham是根据费米能量来选择势能的。之后,Slater提出在交换势能(1.16)中引入一个系数$\alpha$,该系数是通过拟合参数得到的(因此成为$\chi_\alpha$交换势能):
\[V_{\chi_{\alpha}} = \alpha V_{XS}(\vec{r}) \qquad (1.18)\]因此在$\chi_\alpha$方法中,体系的总能量包含一个负的交换势能的组成部分(线性依赖参数$\alpha$),能量最小化不允许确定$\alpha$,只有当参数$\alpha$越高时,总能量越低。
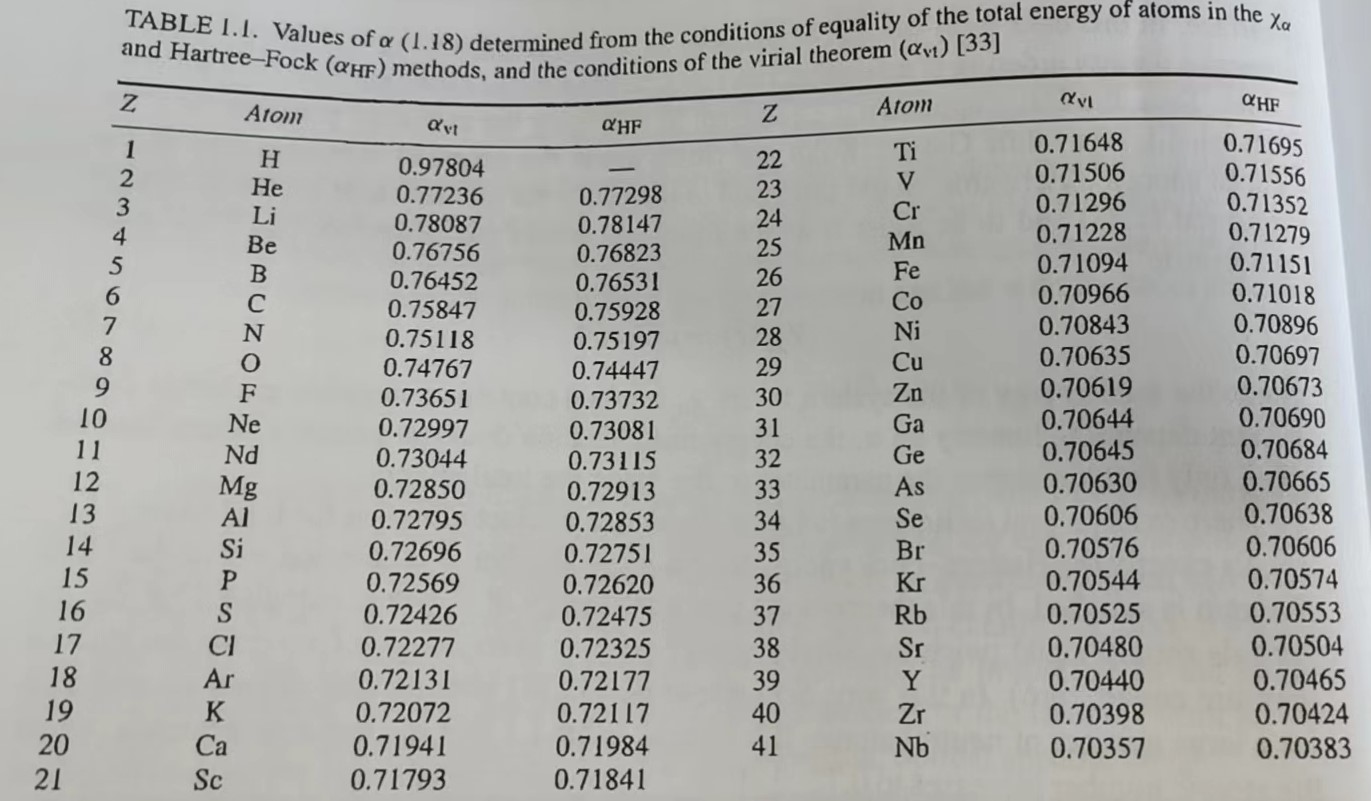
有几种方法可以计算$\alpha$。其中的一种是选择适当的$\alpha$使原子的总能量$E_{\chi_{\alpha}}$精确地等于Hartree-Fock的能量。另外一种方法是选择适当的$\alpha$使维里定理成立。在该理论中,当,通过$\chi_\alpha$轨道计算得到的一个体系的势能等于动能的两倍,但是符号相反(假如体系的压腔等于0)。在这种方法中,Schwarz等人获得了大部份中心原子的$\alpha_{vt}$和$\alpha_{HF}$。从Table 1.1中可以看到:对于3d金属原子,当原子序数增加时,$\alpha_{vt}$和$\alpha_{HF}$会降低到0.72-0.70,然后随着原子序数的增加缓慢下降。主要注意的是,$\alpha_{vt}$和$\alpha_{HF}$的差是无意义的。在一个相似的计算中,遍历了整个元素中期表,如Fig. 1.2所示。
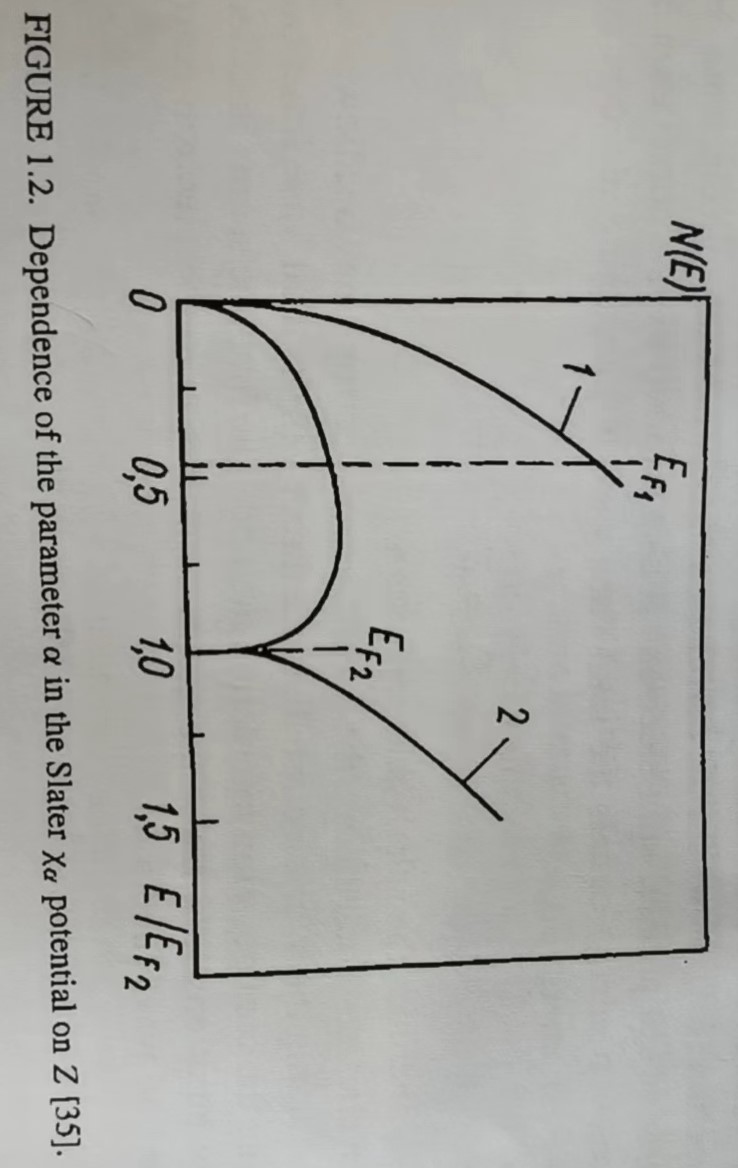
现在,Slater势能的成功之处已经十分清楚了。在能带理论发展的早期阶段,计算通常是非自洽的,使用全Slater交换势能,$\alpha=1$。随后,使用(1.18)的势能的自洽计算方法可以到和之前相同的结果。需要注意的是,当使用变分原理时,借助由自洽问题的解决方案产生的轨道确定的总能量将小于使用任何其他轨道计算的总能量。于此相反,在$\alpha=1$处获得的势能比较小的$\alpha$处获得的更深(Table 1.1)。实际上,这两个相反的效应完全可以取得平衡,至少是在计算过渡金属的能带时。这种偶然的错误的相互抵消使得近二十年来获得了正确的物理结果。然而,全部的补偿没有在过渡金属复合物中发现,并且,在这种情况下,必须使用(1.18)的势能进行自洽计算。
对Hartree-Fock理论而言,很多物理现象不充分描述的另外一个原因是没有考虑足够的关联效应。在实际的体系中,一个电子的运动与其他电子的运动相关。由于库伦排斥作用,两个电子相互靠近时将消耗能量,在(1.4)式中,当$\vec{r} \to \vec{r}’$时$V_C(\vec{r})\to \infty$ 。这允许假设每个电子都被一个库伦空穴包围。
通过Pauli原理,因为不超过一个电子可能占据一个量子态,我们可以类比库伦空穴来谈论费米空穴。因此,Hartree-Fock波函数(1.5)只允许平行自旋电子的相关性。在其他地方,反平行自旋电子的相关性也被称为一个相关性。通过定义,相关能等于一个相互作用的电子系统的总能量减去Hartree-Fock能量$E_{HF}$:
\[E_c=E-E_{HF} \qquad (1.19)\]在这里,$E_{HF}$包括相对论修正。
在Hartree-Fock理论中,电子的相关性可以通过两种方法计算:直接在体系的总的波函数中引入电子间的距离,使用构型相互作用理论(configuration interaction method)。前者看起来是是合理的,因为成对构型(pairwise configuration)是电子相关能的主要贡献。然后,实验性的波函数为:
\[\Psi_c=W\Psi \qquad (1.20)\]其中,$\Psi$是Hartree-Fock方法中使用的Slater行列式。$W$函数可以用两电子函数$u(r_i,r_j)$构建:
\[W=exp\frac{1}{2} \sum_{i<j} u(r_i, r_j) \qquad (1.21)\]现在,必须要使用变分原理来同时优化$u$和$\Psi$。然而,两电子函数违背了$\Psi_c$的正交性,使上述过程变得复杂。为了简化这个函数,$\Psi$定义为粒子间无相互作用的气体,比如对于$u=0$,并且$u$被写成忽略了对自旋的依赖的形式。这种形式在中被使用处理均质电子气。使用的函数$u$的形式为:
\[u(r)=-\frac{1}{4\pi r}[1-exp(-br)]\]其中,$b \sim k_F$可以使用数值变分得到,作者得到的结果与Vashishta和Singwi报道的相同。这种方法有一个简短的综述可以参考。
构型相互作用理论(configuration interaction method)广泛应用于原子计算。在该方法中,波函数被写成行列式函数的线性组合,可以通过单电子自旋轨道波函数得到:
\[\Psi_c = \sum_{K}C_K \Psi(K) \qquad (1.22)\]这里,$\Psi(K)$是由$N$个电子组成的系统的不同构型$K$的 Slater 行列式(1.5)。对上式的主要贡献来自由Hartree-Fock方程导致的行列式,即主要的行列式。其他行列式是通过将主行列式的一个或几个轨道替换为与主要行列式的所有主行列正交的其他轨道而得出的。将(1.22)式带入道(1.6)中得到系数$C_K$和能量$E$的无限线性方程组,当然,必须要截断。随着构型的增加,计算得越精确。如果轨道$\varphi_i(\vec{r})$和系数$C_K$同时变化,计算的结果将会更精确。
应用于原子中,该理论得严格形式可以参考。该方法最主要得劣势在于它非常复杂,难以处理,为了确保足够得精度必须要计算很多行列式。
自洽场和构型相互作用理论都可以靠电子的相关性,显著地提高Hartree-Fock计算的精度。但是它们只能应用在有效的多粒子系统中,比如自由原子。对于晶体,必须要使用Slater $\chi_\alpha$近似。Bohm和Pines已经表明在考虑电子相关性后,交换能强烈依赖于$\vec{k}$的现象消失,然而使用Hartree-Fock方法将会产生该现象。这是$\chi_\alpha$近似的独特的成功之处。
Reference
- Nemoshkalenko V V, Antonov N V. Computational methods in solid state physics[M]. CRC Press, 1999.