固体物理的计算理论: S1-理想晶体中的电子态-1.1.3 密度泛函理论

Computational Methods in Solid State Physics

Nemoshkalenko V V, Antonov N V

数学形式

  密度泛函理论（DFT）是基于Hohenberg和Kohn定理发展而来的，该定理表明：相互作用的电子气的所有基态性质可以通过引入电子密度$\rho(\vec{r})$的泛函来描述。体系的哈密顿可以表示为：

\[E[\rho]=\int d \vec{r} \rho(\vec{r}) \nu_{ext} (\vec{r})+\iint d \vec{r} d \vec{r}^{\prime} \frac{\rho(\vec{r}) \rho\left(\vec{r}^{\prime}\right)}{\left|\vec{r}-\vec{r}^{\prime}\right|}+G[\rho] （1.23）\]

其中$\nu_{ext}(\vec{r})$是原子核所产生的外场，$G[\rho]$包括电子的动能和交换-关联能。体系的总能可以通过对函数求极值得到，$\delta E[\rho]_{\rho = \rho_0(\vec{r})} = 0$，$\rho_0$是电荷的分布。因此，为了求得体系的总能$E$，我们不需要知道所有电子的波函数，得到能量对$\rho$的泛函就够了，然后定义其最小值。需要注意的是：$G[\rho]$是通用的，不依赖任何一个外场。

  Sham和Kohn深入地发展了这种想法，他们表明$G[\rho]$应具有以下形式：

\[G[\rho] = T[\rho] + E_{XC}[\rho] (1.24)\]

其中$T[\rho]$是密度为$\rho(\vec{r})$无相互作用电子地动能；$E_{XC}[\rho]$泛函包含Hartree理论中没有的多电子效应，交换和关联能。

  电子密度为：

\[\rho(\vec{r})=\sum_{i=1}^{N}\left|\varphi_{i}(\vec{r})\right|^{2} （1.25）\]

其中N是体系的电子数。新的变量$\varphi_i$（服从通常的归一化条件）满足：

\[\left[-\nabla^{2}-\sum_{I} \frac{2 Z_{I}}{\left|\vec{r}-\vec{R}_{I}\right|}+\int 2 \frac{\rho\left(\vec{r}^{\prime}\right)}{\left|\vec{r}-\vec{r}^{\prime}\right|} d \vec{r}^{\prime}+V_{\mathrm{xc}}(\vec{r})\right] \varphi_{i}=\varepsilon_{i} \varphi_{i} （1.26）\]

其中，$\vec{R}I$是原子$I$的位置，带有电荷为$Z_I$，$\varepsilon_i$为形成单电子态能谱的Lagrange因子。交换关联势$V{XC}$是能量泛函的微分：

\[V_{\mathrm{xc}}(\vec{r})=\frac{\delta E_{\mathrm{xc}}[\rho]}{\delta \rho(\vec{r})} （1.27）\]

从（1.26）中我们可以发现电子密度$\rho(\vec{r})$和体系的基态总能。

  尽管，DFT在基态被严密地证明，对于交换-关联能泛函目前只能近似得到，该理论对于实际应用的重要性不容小觑，因为它把多电子问题降低为本质上带有有效局域势的单电子问题：

\[V(\vec{r})=-\sum_{I} \frac{2 Z_{I}}{\left|\vec{r}-\vec{R}_{l}\right|}+\int 2 \frac{\rho\left(\vec{r}^{\prime}\right)}{\left|\vec{r}-\vec{r}^{\prime}\right|} d \vec{r}^{\prime}+V_{\mathrm{xc}}(\vec{r}) （1.28）\]

显然，（1.26）式可以使用自洽的方式求解，因为$V(\vec{r})$依赖于我们想要的轨道$\varphi_i(r)$。

  公式（1.23-5）是精确的，因为他们精确定义了电子密度和总能，当然我们需要知道精确的$E_{XC}(\rho)$泛函。所以，DFT应用的核心问题是如何定义或者选择$E_{XC}(\rho)$泛函。对于非均匀电子气，$E_{XC}(\rho)$精确的形式可以写为带有周围交换-关联空穴的电子与电荷密度，$\rho_{XC}(\vec{r}, \vec{r}^{\prime}-\vec{r})$，的库伦相互作用：

\[E_{\mathrm{xc}}[\rho]=\frac{1}{2} \int d \vec{r} \rho(\vec{r}) \int d \vec{r}^{\prime} \frac{\rho_{\mathrm{xc}}\left(\vec{r}, \vec{r}^{\prime}-\vec{r}\right)}{\left|\vec{r}-\vec{r}^{\prime}\right|} (1.29)\]

其中，$\rho_{XC}$定义为：

\[\rho_{\mathrm{xc}}\left(\vec{r}, \vec{r}^{\prime}-\vec{r}\right)=\rho\left(\vec{r}^{\prime}\right) \int_{0}^{2} d \lambda\left[g\left(\vec{r}, \vec{r}^{\prime} ; \lambda\right)-1\right] （1.30）\]

其中，$g\left(\vec{r}, \vec{r}^{\prime} ; \lambda\right)$是对关联函数，$\lambda$是耦合常数。

  $E_{XC}(\rho)$不依赖于交换-关联空穴的实际形状，我们可以把$\vec{R} = \vec{r}^{\prime}-\vec{r}$带入可得：

\[E_{\mathrm{xc}}[\rho]=4 \pi \int d \vec{r} \rho(\vec{r}) \int \vec{R} d \vec{R} \bar{\rho}_{\mathrm{xc}}(\vec{r}, \vec{R}) （1.31）\]

并且之依赖球平均电荷密度：

\[\bar{\rho}_{\mathrm{xc}}(r, R)=\frac{1}{4 \pi} \int d \Omega \rho_{\mathrm{xc}}(\vec{r}, \vec{R}) （1.32）\]

这意味着库伦能只依赖于距离而非方向。而且，空穴电荷密度满足求和规则：

$$4 \pi \int R^{2} d R \bar{\rho}_{\mathrm{Xc}}(r, R)=-2 (1.33)$

这意味着交换相关空穴对应于电子周围的电荷密度减一，这恰好等于电子的电荷。

局域密度近似

  在计算能带的时候，通常要对交换-关联势$V_{XC}(\vec{r})$使用某一个近似。最简单，使用频率最多的是局域密度近似（local density approximation，LDA），$\rho_{XC}(\vec{r}, \vec{r}^{\prime}-\vec{r})$的形式与均与电子气的相似，但是使用电荷密度$\rho(\vec{r})$的局域值来代替空间中每点的密度：

\[\rho_{XC}(\vec{r}, \vec{r}^{\prime}-\vec{r}) = \rho(\vec{r}) \int_{0}^{2} d \lambda\left[g_{0}\left(\left|\vec{r}-\vec{r}^{\prime}\right|, \lambda, \rho(\vec{r})\right)-1\right] (1.34)\]

其中 $g_{0}( | \vec{r}-\vec{r}^{\prime} |, \lambda, \rho(\vec{r}) )$ 是均匀电子气系统对关联函数。该近似满足（1.33）式，这是它基本的优势之一。将（1.34）式带入到（1.29）中，我们可以得局域电子密度近似：

\[E_{\mathrm{xc}}[\rho]=\int \rho(\vec{r}) \varepsilon_{XC}(\rho) d \vec{r} (1.35)\]

其中，$\varepsilon_{XC}$是交换和关联对密度为$\rho(\vec{r})$的均匀相互作用的电子气的总能（每个电子）的贡献。该种近似对应于每个电子都被一个交换相关空穴包围，并且正如预期的那样，当$\rho(\vec{r})$变化缓慢时，该近似表现较好。使用不同方法计算得到的$\varepsilon_{XC}$的结构彼此相差百分之几。因此，我们认为$\varepsilon_{XC}$的值已经足够好了。Hedin和Lundqvist给出了$\varepsilon_{XC}$的插值表示。在LDA中，有效势（1.28）为

\[V(\vec{r})=-\sum_{I} \frac{2 Z_{I}}{\left|\vec{r}-\vec{R}_{I}\right|}+\int 2 \frac{\rho\left(\vec{r}^{\prime}\right)}{\left|\vec{r}-\vec{r}^{\prime}\right|} d \vec{r}^{\prime}+\mu_{\mathrm{xc}}(\vec{r}) (1.36)\]

其中，$\mu_{\mathrm{xc}}(\vec{r})$是局域密度为$\rho(\vec{r})$的均与相互作用电子气的化学势的交换-关联部分：

\[\mu_{\mathrm{xc}}(\vec{r})=\frac{d \rho \varepsilon_{\mathrm{xc}}(\rho)}{d \rho} （1.37）\]

  对于自旋极化的系统，可以使用局域自旋密度近似（LSDA）[ref-8, 45]：

\[E_{XC}\left[\rho^{+}, \rho^{-}\right]=\int \rho(\vec{r}) \varepsilon_{XC}\left(\rho^{+}(\vec{r}), \rho^{-}(\vec{r})\right) d \vec{r} （1.38）\]

其中，$\varepsilon_{XC} (\rho^{+}, \rho^{-})$是均匀电子气系统中每个电子的交换-关联能能，$\rho^{+}(\vec{r})$和$\rho^{-}(\vec{r})$分别是自旋向上和自旋向下的电荷密度。

  需要注意：LDA和LSDA都不包括拟合系数。进一步，因为DFT没有小参数，通常不做不同近似方法结果精度的理论分析。因此，在实际系统中，不同交换-关联势的近似得到的结果需要和实验对比，通常两者的差需要满足一定的容忍度。

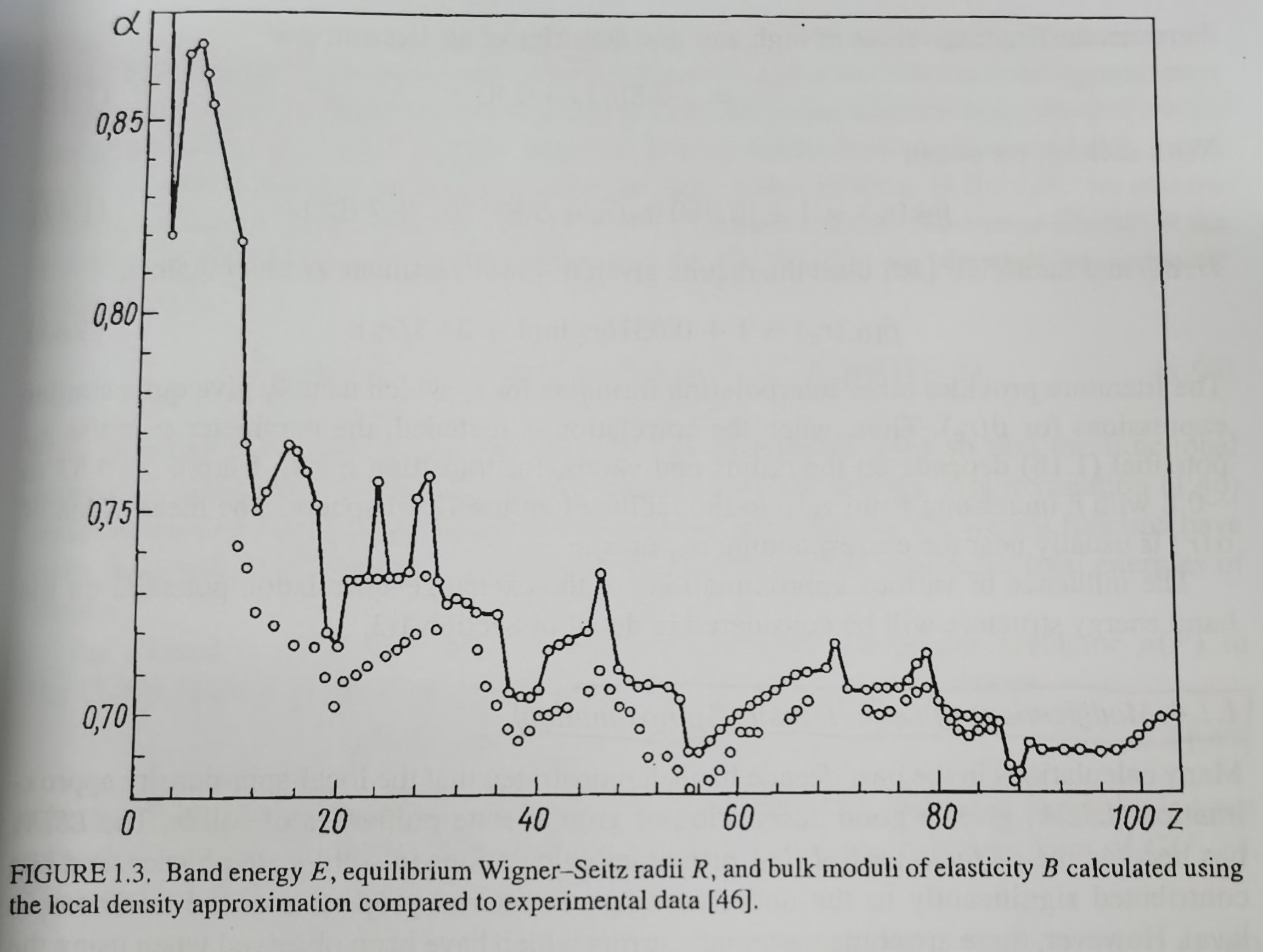
  Fig. 1.3是LDA计算过渡金属基态的精度。该图表示26种过渡金属的结合能，原子密度，和体积模量的实验和理论结果。可以看到，对于磁性3d金属，Cr，Mn，Fe，Co和Ni，理论结果和实验相差较大。进一步的研究表示误差主要是由于没有正确计算磁序，如果计算正确，固体的总能将会降低。

  上述的例子非常重要，Fig. 1.3的结果只是改变一个参数，即每个原子$Z$的电子数量。大体上，LDA的计算可以较好描述金属的基态。

  在量子力学的多粒子系统种，存在两个不同的问题：宏观多粒子系统和原子系统或者几个原子的团簇。宏观系统包含$N \approx 10^{23}$个粒子，发生在$N^{-1}$或者$N^{-1/3}$尺度的效应非常小，可以忽略。对于$N$为10到100的原子或者团簇系统不能忽略上述的效应。此外，在一个自由原子或团簇的边界处发现了电子密度中的强烈变换，然而在金属中，原子周围的电子密度随距离变化比较缓慢。

  对于有限系统（原子和团簇），使用LDA计算的总能的误差大概在5到8%。即使对于简单的系统，如氢原子系统，总能的计算为0.976 Ry，而不是1.0 Ry。因此，有限的多粒子系统需要其他的方法。

  因为金属是宏观的多粒子系统，LDA对基态和电子密度的计算结果不足够好。

  DFT用比Hartree-Fock-Slater方法更自然的方式包括交换和关联效应。这里，交换关联势$V_{XC}$被表示为：

\[V_{\mathrm{xc}}(\vec{r})=\beta\left(r_{\mathrm{e}}\right) V_{\mathrm{GKS}}(\vec{r}) (1.39)\]

这里，$V_{GKS}$是Gaspar-Kohn-Sham势，$r_e$为：

\[r_{\mathrm{e}}(r)=\left[\frac{3}{4 \pi} \rho(r)\right]^{1 / 3} （1.40）\]

该参数在数量级上对应于粒子的势能与其平均动能的比值。

  在（1.39）中，$V_{GKS}$包括了交换效应，然而，素有的关联效应包括在依赖电子密度的因子$\beta(r_e)$中。Wigner表明中等电子密度的关联能可以通过在高等和低等的电子气的电荷密度的限制值之间插值获得：

\[\varepsilon_{\mathrm{c}}=-0.88 / r_{\mathrm{e}}+7.8 （1.41）\]

这样的$\varepsilon_{\mathrm{c}}$，我们可以获得：

\[\beta_{\mathrm{W}}\left(r_{\mathrm{e}}\right)=1+\left[0.9604 r_{\mathrm{e}}\left(r_{\mathrm{e}}+5.85\right) /\left(r_{\mathrm{e}}+7.8\right)^{2}\right] （1.42）\]

Hedin和Lundqvist使用之前的结果估算$\varepsilon_{\mathrm{c}}$，得到：

\[\beta_{\mathrm{HL}}\left(r_{\mathrm{e}}\right)=1+0.0316 r_{\mathrm{e}} \ln \left(1+24.3 / r_{\mathrm{e}}\right) （1.43）\]

文献了提供了其他的插值公式来获得$\varepsilon_{\mathrm{c}}$，通常和$\beta(r_e)$的表达式非常接近。因此，当包含相关效应时，$\chi_\alpha$势（1.18）中的$\alpha$依赖半径，对于过渡金属来说，当半径$r$从零增加到一个内切球的半径时，$\alpha$从0.67变化到0.8。$\alpha(r)$的平均值通常近接相对应的$\alpha_{vt}$或$\alpha_{HF}$。

  交换-关联势的不同近似ui能带结构的影响将在1.3章节详细讨论。

微信公众号

Reference

• Nemoshkalenko V V, Antonov N V. Computational methods in solid state physics[M]. CRC Press, 1999.